1) INTRODUÇÃO
Não se pode imaginar a humanidade sem a circunferência, ou
círculo. Como seria o mundo sem
rodas? Podemos afirmar que ainda hoje
com todas as tecnologias avançadas que possuímos, a roda inventada há 3.500 a .C faz-se presente e
desempenha um papel importantíssimo.
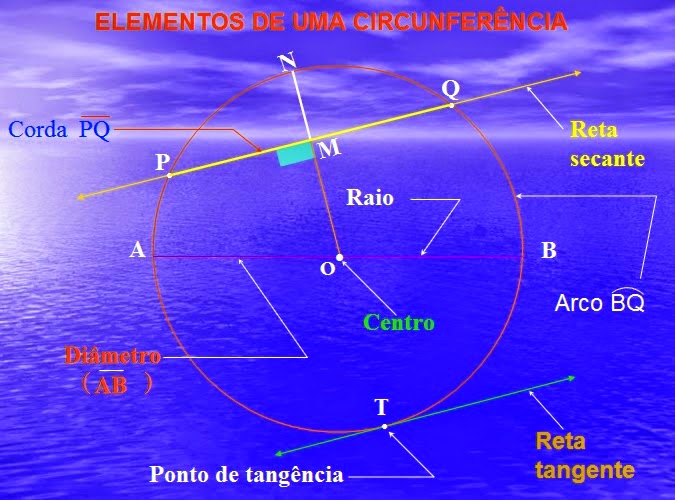
2) Circunferência e círculo
Circunferência, ângulo central, círculo e
setor circular
Circunferência é o lugar geométrico dos
pontos de um plano que equidistam de um ponto fixo. O ponto fixo é o centro e a
equidistância o raio da circunferência
Ângulo central em
uma circunferência é todo ângulo que tem como vértice o centro dessa
circunferência
Círculo ou disco é o conjunto dos pontos internos de uma circunferência.
Setor circular é
qualquer uma das partes do círculo determinados por um ângulo central.
3) Gráfico de setores
4) Divisão da circunferência em partes iguais e do círculo em
setores iguais
Usando régua, compasso e transferidor
Processo de Rinaldini para a divisão da circunferência em n
partes iguais.
Por exemplo: Seja dividir a circunferência em 9 partes
iguais.
a- Traçamos o diâmetro AB e o dividimos em 9 partes,
assinalando porém, sómente os pontos alternados, 2, 4, 6 e 8.
b- Com raio igual ao diâmetro AB, e com centro em A e B, construímos arcos que se interceptam em P e Q.
c- As retas P2, P4, P6 e P8,
encontram a circunferência no semi-plano oposto em relação a AB, os
primeiros 4 pontos da divisão. Pelo outro lado, Q2, Q4, Q6
e Q8, completam a divisão desejada.
Por se tratar de um processo aproximado, não podemos repetir
sucessivamente uma só corda ao longo da circunferência. O uso dos pontos P e Q
são fundamentais na distribuição do erro.
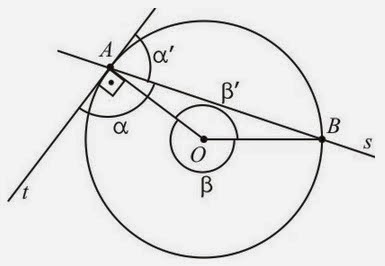
5) Posições relativas de uma reta e de uma circunferência
Reta s tangente à
circunferência:
Qualquer reta tangente é perpendicular ao raio no ponto de
tangência.
Distância entre a reta s
e o centro da circunferência é igual ao raio.
Reta s secante à
circunferência:
Distância entre a reta s
e o centro da circunferência é menor que o raio.
Reta s externa à
circunferência:
Distância entre a reta s
e o centro da circunferência é maior que o raio.
Circunferência inscrita e circunscrita a
um polígono
Circunferência inscrita é tangente aos lados do polígono.
Circunferência circunscrita é aquela que passa pelos
vértices do polígono.
6) Posições relativas entre um ponto e uma circunferência
7) Posições relativas de duas circunferências
8) Ângulos em uma circunferência
Ângulo central e inscrito
Ângulo central e inscrito e ângulo de
segmento
α = ângulo de
segmento.
Prova-se que um ângulo de segmento e um ângulo inscrito têm
medidas iguais quando o arco correspondente é o mesmo.
α = ângulo de segmento
é obtuso.
Continua valendo todas as relações vistas anteriormente.














Parabéns pela iniciativa!
ResponderExcluirArrasou!!!!
ResponderExcluir