Matemática8-ThiagoKYamamoto: Geometria e Álgebra

1) Determine a área das seguintes figuras (em cm):

Resp.: 38,5 cm²

Resp.: 99 cm²

2) Sabendo que a área de um quadrado é 36cm², qual é seu perímetro?

Resp.: 24 cm

3) Encontre as medidas dos ângulos x e y do triângulo equilátero abaixo, sabendo que BN e CM são bissetrizes dos ângulos B e C , respectivamente.

Resp.: x = 120º, y = 60º

4) Qual o valor de x indicado na figura?

Resp.: x = 28º

5) Determine as medidas dos ângulos x, y e z indicadas no triângulo abaixo, sabendo que as semirretas AP e CK são bissetrizes.

Resp.: x = 30º, y = 50º, z = 80º

6) Sabendo-se que o triângulo abaixo é isósceles, determine o valor de x.

Resp.: x = 40º

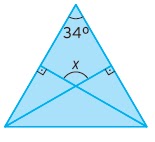
7) Calcule a medida do ângulo obtuso formado pelas alturas relativas aos lados congruentes de um triângulo isósceles, sabendo que o ângulo do vértice mede 34°.

Resp.: x = 146º

8) Calcule a medida dos ângulos internos de um triângulo isósceles, sabendo que a altura relativa à base e a bissetriz de um ângulo interno formam um ângulo de 72°.

Resp.: 36º, 36º, 108º

9) Determine o valor do ângulo x. Sabendo-se que o triângulo abaixo é retângulo em A, e AB = AE = AD.

Resp.: x = 45º

10) Determine o valor do ângulo x da figura abaixo:

Resp.: x = 70º

11) Determine os valores de x e y. Sabendo-se que a semireta AS é bissetriz do ângulo BÂC.

Resp.: x = 12º, y = 40º

12) Determine o valor do ângulo DÊC. Sabendo-se que na figura abaixo, o triângulo ABC é isósceles de base BC e o triângulo ADE é isósceles de base DE e sendo ângulo BÂE = 46º.

Resp.: DÊC = 23º

13) Na figura, o ângulo C é reto, D é ponto médio de AB, DE é perpendicular a AB, AB = 20cm e AC = 12cm. Calcule a área do quadrilátero ADEC.

Resp.: 58,5 cm²

14) Uma corda de 3,9 m de comprimento conecta um ponto na base de um bloco de madeira a uma polia localizada no alto de uma elevação, conforme o esquema abaixo. Observe que o ponto mais alto dessa polia está 1,5 m acima do plano em que esse bloco desliza. Caso a corda seja puxada 1,4 m, na direção indicada abaixo, qual será a distância x que o bloco deslizará?

Resp.: 1,6 m

15) Na figura abaixo, os comprimentos dos lados AB e BC do triângulo ABC são iguais. Determine o valor do ângulo α.

Resp.: 20º

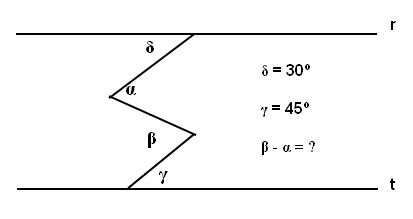
16) Sejam r e t retas paralelas. A medida do ângulo δ é 30° e a medida do ângulo γ é 45°. Qual é valor da medida de (β – α) ?

Resp.: 15º

17) Em um triângulo retângulo, a hipotenusa é 5/3 do tamanho do cateto menor. O cateto maior tem tamanho igual a 4/3 do cateto menor. Sendo 60 cm o perímetro desse triângulo, qual é sua área?

Resp.: 150 cm²

18) Considere um triangulo retângulo com hipotenusa medindo 15 cm, um dos catetos medindo 9 cm e perímetro de 36 cm. Pergunta-se: qual é sua área?

Resp. 54 cm²

19) Uma região de uma cidade possui o formato de um setor circular. Os pontos A, B e C são esquinas, a distância entre os pontos A e B é de 1 km e o ângulo formado pelas ruas 1 e 2 é de 120º, conforme mostra a figura abaixo. João e Marcos desejam ir do ponto B para o ponto C. Para tanto, João percorreu as ruas 1 e 2, passando inicialmente por A, enquanto Marcos seguiu o trajeto da Rua 3. Calcule a distância que cada um percorreu, considerando pi=3,14.

Resp.: João=2km, Marcos=2,09km

20) Na figura abaixo calcule a área em verde, sendo que temos um quadrado com e círculos inscritos, de raio R, em 2 de seus quadrantes. A área deve estar na expressão algébrica mais simples.

Resp.: 2R² ( 8 – π)

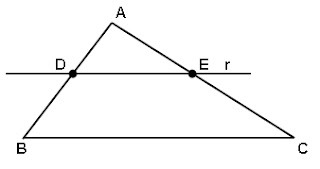
21) A figura representa uma chapa de alumínio de formato triangular de massa 1 250 gramas. Deseja-se cortá-la por uma reta r paralela ao lado BC , que intercepta o lado AB em D e o lado AC em E, de modo que o trapézio BCED tenha 700 gramas de massa. A espessura e a densidade do material da chapa são uniformes. Determine o valor percentual da razão de AD por AB.

Dado: √11=3,32

Resp.: 66,4 %

22) Calcule o ângulo α da figura abaixo. Sendo que temos um quadrado, pentágono regular e hexágono regular colados.

Resp.: 42º

23) Na figura, as retas r e t são paralelas, o ângulo 1 mede 45° e o ângulo 2 mede 55°. A medida em graus, do ângulo 3 é:

Resp.: 100º

24) O triângulo retângulo ABC, da figura, representa um terreno com área igual a 760 m2. A região em azul foi demarcada para construção de uma casa e o restante do terreno ficou reservado para lazer. Sabendo-se que M e N são pontos médios dos catetos do triângulo ABC, calcule a área do triângulo ONC , em m2.

Resp.: 190 m²

25) Uma fonte luminosa a 25 cm do centro de uma esfera projeta sobre uma parede uma sombra circular de 28 cm de diâmetro, conforme figura abaixo.

Se o raio da esfera mede 7 cm, calcule a distância (d) do centro da esfera até a parede, em cm.

Resp.: 23 cm

26) Determine o valor da área do quadrado inscrito no triângulo retângulo do desenho; sabendo-se que o segmento OC=6*√5 e 2*BC=3*NC=6*ON.

Resp.: 36

27) Um marido apaixonado resolveu prestar uma homenagem à sua esposa, construindo um jardim em forma de um coração, conforme ilustra a figura. Para construí-lo, ele utilizou mudas de flores vermelhas na razão de 200 mudas por metro quadrado. Calcule o total de mudas utilizadas na montagem de tal jardim. (Use pi = 3,14)

Resp.: 5712

28) Os vértices do triângulo ∆XYZ são pontos médios dos lados do triângulo eqüilátero ∆ABC cujos lados medem 2 m. Se h₁ e h₂são, respectivamente, alturas dos triângulos ∆XYZ e ∆ABC, então determine o produto h₁.h₂ em m².

Resp.: 1,5 m²

29) A altura do triângulo equilátero de vértice A, B, C, representado pela figura, é h₂ = 3√3. Sendo X, Y, Z os pontos médio dos lados do ∆ABC. Calcule a área do triângulo ∆XYZ, supondo que os lados ∆ABC são iguais a 6.

Resp.: (9√3)/4

30) Sendo ABCDE um pentágono regular, calcule a soma dos ângulos assinalados na figura.