
René Descartes (1596 –
1650) Filósofo e Matemático. Acreditava
que o cálculo com expressões algébricas era um método poderoso e universal para
resolver problemas.
Cálculo algébrico é aquele que envolvem as
expressões algébricas.
Expressões
algébricas: são aquelas que contêm números e letras
(=variáveis).
Ex.: 2ax² + bx +3
Valor numérico de uma
expressão algébrica: é o número que obtemos substituindo as variáveis por
números e efetuamos suas operações.
Variáveis: são
letras das expressões algébricas que representam um número real e que de
princípio não possuem um valor definido.
1)
EXPRESSÕES ALGÉBRICAS INTEIRAS
São aquelas que não têm incógnitas no denominador ou dentro de radicais.
(considerando apenas o “x” como incógnita e sendo “a” e “b” valores conhecidos).
Ex.:
2)
MONÔMIOS
São expressões algébricas que os números e
letras estão ligados por produtos.
Ex.: 4x, 2x², 2ab³
Grau de um monômio:
é dado pela soma dos expoentes da parte literal. Ex.: +
5x²y³ é de grau 5. Ou, também, pode ser
dado em relação a uma das letras (=variáveis). Ex.: - 5x²y³ é de grau 2 a x e é de grau 3 a y.
3)
MONÔMIOS SEMELHANTES OU TERMOS SEMELHANTES
São chamados de monômios semelhantes ou termos semelhantes,
quando apresentam a mesma parte literal. Ex.: x³, 8x³, 11x³, 55x³ (a parte x³ é
parte igual para todos os monômios).
4)
OPERAÇÕES COM
MONÔMIOS
Adição e Subtração de Monômios semelhantes
Adição: I) 2x + 3x = (2 + 3).x = 5.x = 5x
Subtração: I) 2x – 3x = (2 – 3).x = -1.x = -x
Atentar no jogo de
sinais:
( x³ + 2 y² + 1 ) – ( y ² - 2 ) = x³ +2 y² + 1 – y² + 2 = x³ +
y² +3
Multiplicação de monômios
I) (9x²).(5x³) = (9.5)(x².x³) =
45x²+3 = 45x5
II) (3x).(-4y) = (3.(-4)).(x.y)
= -12.(x.y) = -12xy
Para multiplicarmos potências de mesma base, conservamos a
base e somamos os expoentes.
Divisão de monômios
I) (12x6) : (3x²) = 12x6/3x² = 12/3.x6/x²
= 4.x6-2 = 4x4
II) 21x³y / 7xy =
21/7.x³/x.y/y = 3.x³-1.y1-1 = 3.x².1 = 3x²
Na divisão de potências devemos conservar a base e subtrair os
expoentes.
Potenciação de monômios
I) (5x³)² = 5².(x³)² = 25.x3.2 = 25x6
II) (-2xy²)³ = (-2)³.x³.(y²)³ = -8.x³.y2.3 = -8.x³.y6
5)
POLINÔMIOS
Toda expressão que indica uma soma algébrica (adição ou
subtração) de monômios não semelhantes é chamada de polinômio.
Ex.:
I) 5a² - 3a + 1
II) 4x² - 2xy + 3x
III) 2x + 6
Redução de termos semelhantes
O perímetro de um
canteiro de jardim, representado pela região poligonal acima:
Perímetro: 2x + y + 2x + 2y + 4x + 3y =
EQUAÇÃO DE DIOFANTO

Diofanto
de Alexandria é considerado como o maior algebrista grego, séc III a.C.. (Pai
da Álgebra)
Equação de Diofanto
Um sexto dela foi uma bela infância. Depois de 1/12 da sua vida, a sua barba cresceu. Um sétimo da sua vida passou-se num casamento sem filhos. Mas, cinco anos após isso, nasceu o seu primeiro filho, que viveu uma vida feliz durante apenas metade do tempo de vida do seu pai. E, em profundo pesar, o pobre velho terminou os seus dias na Terra, quatro anos após perder o filho.
Um sexto dela foi uma bela infância. Depois de 1/12 da sua vida, a sua barba cresceu. Um sétimo da sua vida passou-se num casamento sem filhos. Mas, cinco anos após isso, nasceu o seu primeiro filho, que viveu uma vida feliz durante apenas metade do tempo de vida do seu pai. E, em profundo pesar, o pobre velho terminou os seus dias na Terra, quatro anos após perder o filho.
Grau de um polinômio
O grau de um
polinômio é numericamente igual à soma dos expoentes da parte literal do seu
termo de maior grau depois de reduzidos seus termos semelhantes.
Exemplos:
a) 4x³ − 3x² + 5 é um polinômio de 3º grau,
pois, 4x³ é seu termo de maior grau;
b) 2x + xy – 6y é um polinômio de 2º grau, pois,
xy é seu termo de maior grau.
Operações com polinômios
Adição (=soma) e Subtração (=diferença)
Dados os polinômios
P= 3x² + 2x e Q= 2x² + x, vamos indicar a soma e diferença, respectivamente: P
+ Q e P – Q.
Soma: P+Q =
(3x² + 2x) + (2x² + x) = 3x² + 2x + 2x² + x = 5x² + 3x
Diferença: P-Q =
(3x² + 2x) - (2x² + x) = 3x² + 2x -1•( 2x² + x)
= 3x² + 2x − 2x² − x = x² + x
Polinômios opostos ou simétricos
Exemplo: os polinômios P = 3x² − 5x + 10 e Q = − 3x² +
5x – 10 são simétricos, pois a sua soma
resulta em um polinômio nulo.
P = 3x² − 5x + 10 =
(3x² − 5x + 10)
Q = − 3x² + 5x – 10
= − (3x² − 5x + 10)
P + Q = (3x² − 5x +
10) − (3x² − 5x + 10) = 0
Multiplicação
Monômio por polinômio
Utilização da
propriedade da multiplicação de potências de mesma base:
3x
• x = 3x²
Utilização da propriedade distributiva da multiplicação em
relação à adição.
Exemplo:
-2x
• (x² − 3x + 2) = − 2x³ + 6x²
− 4x
Binômio por binômio
Dois polinômios quaisquer
Divisão
Polinômio por monômio
Lembrete: Todos os divisores devem ser diferentes de zero,
pois não existe divisão por zero.
(6x³ − 12x) : (3x)
→
A condição (3x ≠ 0) é obrigatória.
Polinômio por polinômio
Lembrete: o grau que
aparece no resto deve ser sempre menor do que o grau do polinômio que é
divisor.
Para exemplificar, vamos utilizar o processo da chave para a
seguinte divisão:
(15x² + 2x − 8) ∕ (5x + 4)
1º Passo) Dividimos o 1º termo do dividendo pelo 1º
termo do divisor:
2º Passo) Multiplicamos 3x • (5x + 4) = 15x² + 12x e
subtraímos o valor obtido de 15x² + 12x.
Para tanto, mudamos os sinais de 15x² + 12x e somamos a 15x² + 12x:
3º Passo) Repetimos o processo dividindo o 1º termo
de − 10x − 8 pelo 1º termo de 5x + 4, ou
seja, (−10x) ∕ (5x) = − 2:
4º Passo) Então, (15x² + 2x − 8) ∕ (5x + 4) = 3x − 2.
Prova:
PRODUTOS NOTÁVEIS
Algumas multiplicações que envolvem polinômios apresentam
uma regularidade (um padrão) em seus resultados (produtos). Por isso, são conhecidas como produtos
notáveis.
(a+b)² = (a+b)•(a+b) = a•a + a•b + b•a + b•b = a² + 2ab + b²
O quadrado
da soma de dois termos é igual ao quadrado do 1º termo mais o dobro do produto
do 1º termo pelo 2º termo mais o quadrado do 2º termo.
Exemplo:
(3x +5)² = (3x)² + 2•(3x•5) + 5² = 9x² + 30x + 25
QUADRADO DA
DIFERENÇA: (a − b)² ou (a − b)•(a − b)
(a−b)² = (a−b)•(a−b) = a•a − a•b − b•a + b•b = a² − 2ab + b²
O quadrado
da diferença de dois termos é igual ao quadrado do 1º termo menos o dobro do
produto do 1º termo pelo 2º termo mais o quadrado do 2º termo.
Exemplo:
(7x − 3)² = (7x)² − 2•(7x•3) + 3² = 49x² + 42x + 9
PRODUTO DA
SOMA PELA DIFERENÇA: (a + b)•(a − b)
(a + b)•(a − b) = a•a − a•b + b•a − b•b = a²
− b²
O produto da
soma pela diferença dos mesmos termos é igual ao quadrado do 1º termo menos o
quadrado do 2º termo.
CUBO DA
SOMA: (a + b)³
(a + b)³ = (a + b)•(a + b)² = (a + b)•(a² + 2ab + b²) =
= a³ + 2a²b + ab² + ba² +
2ab² + b³ = a³ + 3a²b + 3ab² + b³
O cubo da
soma de dois termos é igual ao cubo do 1º termo mais o triplo do produto do
quadrado do 1ºtermo pelo 2º termo mais o triplo do produto do 1º termo pelo quadrado
do 2º termo mais o cubo do 2º termo.
Exemplo:
(x + 4)³ = x³ + 3•x²•4 + 3•x•4² + 4³ = x³ + 12x² + 48x + 64
CUBO DA
DIFERENÇA: (a −
b)³
(a − b)³ = (a − b)•(a − b)² = (a − b)•(a² − 2ab + b²) =
= a³ − 2a²b + ab² − ba² + 2ab² − b³ = a³ − 3a²b + 3ab² − b³
O cubo da
diferença de dois termos é igual ao cubo do 1º termo menos o triplo do produto
do quadrado do 1º termo pelo 2º termo mais o triplo do produto do 1º termo pelo
quadrado do 2º termo mais o cubo do 2º termo.
Exemplo:
(x − 4)³ = x³ − 3•x²•4 + 3•x•4² − 4³ = x³ − 12x² + 48x − 64
FATORAÇÃO DE POLINÔMIOS
Fatorar um polinômio
é expressa-lo por meio de uma multiplicação.
1º CASO DE
FATORAÇÃO: fator
comum (colocação de um termo em evidência)
3a² + 3ab = 3a•a
+ 3a•b = 3a•(a + b), logo: 3a² + 3ab = 3a•(a
+ b), sendo 3a•(a+b) é a forma fatorada. Colocamos neste caso 3a em evidência.
Exemplo:
(10x² − 15x) = 5x•2x − 5x•3 = 5x•(2x−3)
Observe: o fator comum em
evidência é sempre o máximo divisor comum entre os termos.
2º CASO DE
FATORAÇÃO: agrupamento
ax + 2a + 5x + 10 =
a(x+2) + 5(x+2) = (x+2)•(a+5)
A fatoração de dois
grupos, separadamente, deve “gerar” um fator comum para uma nova fatoração.
Exemplo:
ab + a − bx − x = a(b+1)-x(b+1) = (b+1)•(a−x)
3º CASO DE
FATORAÇÃO: trinômio
quadrado perfeito
a) x² +10x + 25 = (x+5)² à
(quadrado da soma)
b) a² − 14a + 49 = (a-7)² à
(quadrado da diferença)
4º CASO DE FATORAÇÃO:
diferença entre
dois quadrados
a) (quadrado da soma) à x² −
64 = (x − 8)•(x + 8)
b) 25x² − 81 = (5x + 9)•(5x − 9)
5º CASO DE
FATORAÇÃO: soma de
dois cubos
a) (soma de dois
cubos) à x³ + y³ = (x + y)•(x² − xy + y²)
b) 125x³ + 8 = (5x)³ + 2³ = (5x + 2)•(25x² − 10x
+ 4)
6º CASO DE
FATORAÇÃO: diferença
entre dois cubos
a) (diferença entre dois cubos) à x³ −
y³ = (x−y)•(x² + xy + y²)
b) 27x³ − 125 = (3x)³ − 5³ = (3x − 5)•(9x² + 15x
+ 25)
RESUMO DOS
CASOS DE FATORAÇÃO:
OUTRAS
FORMAS DE FATORAÇÃO:
Há expressões que
podem ser fatoradas mais de uma vez.
Vejamos algun exemplos:
a)
b) 4x³ + 4x² + x = x(4x² + 4x + 1) =
x(2x+1)(2x+1) = x(2x+1)²
c)
x² − y² + 3x + 3y = (x+y).(x-y) + 3(x+y) = (x+y).(x-y+3)
MÍNIMO
MÚLTIPLO COMUM DE POLINÔMIOS:
MMC entre 45x³y e 18xyz:
MMC entre 4x² − 2x e
12x² − 12x + 3:
6. FRAÇÕES ALGÉBRICAS
Definição: Fração
Algébrica é toda fração cujo denominador é uma expressão algébrica.
Exemplos:
1)
Já sabemos que o denominador de uma fração não pode ser ZERO.
Logo, tem-se que:
1)
2)
Simplificação
de Frações Algébricas:
Na simplificação de
frações dividimos o numerador e o denominador pelo mesmo número (diferente de
zero). É mesma coisa que cancelar os
fatores comuns e obter uma fração mais simples.
Exemplos:
a) x e y devem ser diferentes de zero.
b) fatorando o numerador e (x+y) ≠ 0.
c) a ≠ 0
Adição e
Subtração de Frações Algébricas:
Exemplos:
mmc (2x, 4y, 3) = 12xy
mmc
[ (x-y), (x²-y²)] = (x+y).(x-y)
Multiplicação
e Divisão de Frações Algébricas:
Exemplos:
1) Multiplicação:
Análogo à potência de uma fração a um expoente.
Exemplos:











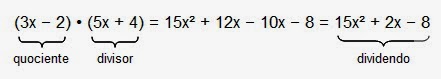












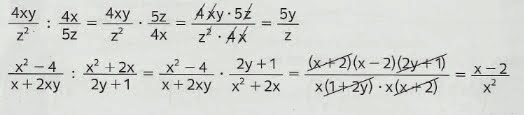

Muito bom :D
ResponderExcluir