1)
Ângulos opostos pelo vértice: 2 ângulos opostos pelo
vértice têm a mesma medida.
) 
Os ângulos α e β são iguais porque são opostos pelo
vértice.
Todos os ângulos opostos vértice são iguais.
Os ângulos α e β são adjacentes e suplementares
(α + β = 180º).
Os ângulos α e γ são opostos pelo vértice (α = γ).
2) Ângulos formados por retas paralelas cortadas por uma
reta transversal.
- Ângulos correspondentes:
(a = e), (b = f), (c = g), (d = h)
- Ângulos colaterais externos:
(a + h = 180º), (b + g = 180º)
- Ângulos alternos externos:
(a = g), (b = h)
- Ângulos alternos internos:
(c =e), (d = f)
- Ângulos colaterais internos:
(c + f = 180º), (d + e = 180º)
3) Soma das medidas dos ângulos internos de um triângulo
Soma
dos ângulos internos do triângulo qualquer é
sempre 180º.
sempre 180º.
Traçar uma reta paralela (que
contém o vértice A) ao
segmento BC (lado BC) e sabemos que os ângulos
alternos
internos são iguais (Lembrar o “Zé” do
zorro, como sempre diz o meu grande
mestre – papai).
4)
Relação que envolve as medidas dos ângulos internos e
externos de um triângulo.
Em todo triângulo, a medida de um ângulo externo é igual
à soma das medidas dos ângulos internos não adjacentes
a ele.
a)
x = m(β) + m(γ)
b)
y = m(α) + m(γ)
c)
z = m(α) + m(β)
5)
POLÍGONOS
Elementos de um polígono convexo:
5.1) Vértices: os pontos A, B, C, D, e F.
5.2) Lados: os segmentos AB, BC, CD, DE, EF e FA.
5.3) Diagonais: os segmentos que ligam um vértice ao outro vértice –
AC, AD, AE, BF, BE, BD, CF, CE e
DF.
5.4) Ângulos internos e Ângulos externos de um polígono
5.4.1) Ângulos internos – são formados por 2 lados consecutivos.
5.4.2) Ângulos externos –
são formados por um lado e o
prolongamento
do lado consecutivo a ele.
Nome de Polígonos quanto ao
número de lados
·
Triângulo
(tri = três) – 3 lados
·
Quadrilátero
(quadri = quatro) – 4 lados
·
Pentágono
(penta = cinco) – 5 lados
·
Hexágono
(hexa = seis) – 6 lados
·
Heptágono
(hepta = sete) – 7 lados
·
Octógono
(octo = oito) – 8 lados
·
Eneágono
(enea = nove) – 9 lados
·
Decágono
(deca = dez) – 10 lados
·
Undecágono
(um + dez) – 11 lados
·
Dodecágono
(dois + dez) – 12 lados
·
Pentadecágono
(cinco + dez) – 15 lados
·
Icoságono
(icos = vinte) – 20 lados
6)
POLÍGONOS REGULARES
polígono convexo.
Onde Si é a soma e n o
número de lados.
Soma da medida de um ângulo interno e ângulo
externo em certo vértice.
Soma das medidas dos ângulos externos de um
polígono convexo.
Em qualquer polígono convexo, a
soma das medidas dos ângulos externos é igual a 360º.
Prova:
Vamos considerar um polígono
convexo de n lados:
Se αi + αe
= 180º, então é verdade escrever que n.( αi + αe) = n.180º,
logo temos que: n.αi + n.αe = n.180º → Si + Se = n.180º →
(n-2).180º + Se =
n.180º →
n.180º - 360º + Se = n.180º
→
Se = n.180º - n.180º +
360º → Se =
360º
Ângulos internos e ângulos externos de
polígonos regulares.
Número de diagonais de um polígono convexo.
7)
Características de um triângulo
·
O triângulo é o único polígono que não tem
diagonal
·
O triângulo é o único polígono rígido
Condição de existência de um
triângulo:
Para que um triângulo exista: b < a + c, c < b + a,
a < b + c.
Congruência de triângulos:
Dois triângulos são congruentes
se houver a igualdade dos 3 ângulos e 3 lados.
8)
Mediana, bissetriz e altura de um triângulo
Mediana
Mediana de um triângulo é o
segmento que tem como extremidades um vértice do triângulo e o ponto médio do
lado oposto a esse vértice.
Na figura: O ponto M é o ponto
médio do segmento BC e o segmento AM é uma mediana do triângulo ABC. Um triângulo possui 3 medianas.
Baricentro de um triângulo
O encontro das medianas de um
triângulo é chamado de BARICENTRO. Em um
triângulo as três medianas se cruzam no mesmo ponto (veja na figura acima: G)
O
baricentro de qualquer triângulo divide a mediana na razão de 1 para 2.
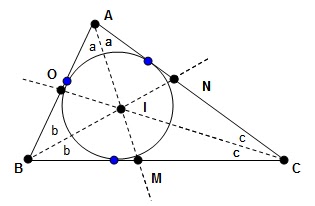
Bissetriz de um triângulo:
O segmento AS divide o ângulo A em 2 ângulos congruentes
(=iguais) e o ponto S pertence ao lado BC.
Incentro de um Triângulo:
O encontro (=cruzamento) das três
bissetrizes do triângulo ABC se chama INCENTRO.
Este ponto I é o centro da
circunferência inscrita no triângulo, em outras palavras, é o centro da
circunferência que toca cada lado em apenas 1 ponto.
Altura de um triângulo:
Em todo triângulo o encontro das alturas, ou
seus prolongamentos é chamado
de Ortocentro.
CIRCUNCENTRO DE UM TRIÂNGULO
mAB = mediatriz do lado AB
mBC = mediatriz do lado BC
mAC = mediatriz do lado AC
O circuncentro é o ponto de encontro
das mediatrizes e este ponto é o centro da circunferência que circunscreve o
triângulo, isto é, é o centro da circunferência que passa pelos 3 vértices do
triângulo.
ORTOCENTRO DE UM TRIÂNGULO
É o ponto de encontro das alturas
de um triângulo.
9)
QUADRILÁTEROS
Paralelogramo
Paralelogramo é todo quadrilátero
cujos lados opostos são paralelos.
·
Em todo paralelogramo, dois ângulos opostos são
congruentes (=medidas iguais) e dois ângulos não opostos são suplementares (α +
β = 180º).
·
Em todo paralelogramo, os lados opostos são
congruentes.
·
Em todo paralelogramo, as diagonais se encontram
no meio.
Losango
As diagonais de um losango são
perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos
do losango.
Trapézio
·
Trapézio retângulo: um dos lados é perpendicular
às duas bases.
·
Trapézio isósceles: os dois lados, que não são
bases (paralelos), são congruentes (tem medidas iguais. Além disso as diagonais são congruentes e os ângulos
adjacentes a uma mesma base são congruentes .
Base média de um trapézio:
O ponto M divide o segmento AD em
duas partes iguais e o ponto N, por sua vez, divide o segmento BC em duas
partes iguais.
10)
Exercícios (vá
para próximo post)
Nenhum comentário:
Postar um comentário